07 선형성을 넘어서

다항식 모델의 종류

다항식 회귀 : 설명변수 각각을 거듭제곱
계단함수 : 변수의 범위를 K개로 나누어 범위별 상수 적합
회귀 스플라인(reqression splines) : X의 범위를 K개 영역으로 나누어 적합
평활 스플라인(smoothing splines): 회귀스플라인과 유사, 평활도 패널티 조건에서 잔차 제곱합을 최소로 적합
국소회귀 : 스플라인과 유사하나, 각 영역이 겹쳐질수 있음(smooth way)
일반화가법모델 : 위의 모델들을 확장

7.1 다항식 회귀

다항식 회귀는 표준적 선형모델(식 1)을 다항식 함수(식 2)로 대체 하는 것.

식 1) $y_i = \beta_0 + \beta_1x_i + \epsilon_i$
식 2) $y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \beta_3x_i^3 + ... + \beta_dx_i^d + \epsilon_i$

여기서 $\epsilon$ 은 오차항이다. 충분히 큰 값의 d에 대해 다항식회귀는 극심하게 비선형적인 곡선을 만든다.

일반적으로는 3또는 4보다 큰 값의 d를 사용하는 경우는 드물다. 곡선이 지나치게 유연해져 아주 이상한 형태를 가질 수 있기 때문이다.

이 결과 역시, 로지스틱 회귀를 사용하여 적합 가능하다.

7.2 계단함수

다항식 함수들을 선형모델의 설명변수로 사용하는것은 X의 비선형 함수에 전역구조(이게 뭐지?)를 도입하는 것이다. 전역구조를 도입하는것을 피하기 위해 계단함수가 사용될 수 있다. X의 범위를 여러개의 bin으로 분할하여 각 빈에 다른 상수를 적합한다. 이것은 연속적인 변수를 순서 범주형 변수 (ordered categorical variable)로 변환하는 것이다.

식 3 $$ C_0(X) = I(X < c_1)

C_1(X) = I(c_1 <= X < c_2)

C_2(X) = I(c_2 <= X < c_3)

...

C_{K-1}(X) = I(c_{K-1} <= X < c_K)

C_K(X) = I(c_K <= X) $$

여기서 I는 조건이 참이면 1 아니면 0을 반환하는 함수이다. 즉, X는 임의의 한 구간에 속하므로 C? 들의 합은 1이 된다. 식 4 와 같이 적합된다.

식 4) $y_i = \beta_0 + \beta_1C_1(x_i) + \beta_2C_2(x_i) + ... + \beta_KC_K(x_i) + \epsilon_i$

역시, 로지스틱 회귀를 사용하여 적합 가능하다.

7.3 기저함수

앞의 모델들은 기저함수(basis function) 기법의 일종이다. 이의 개념은 변수 X에 적용될 수 있는 함수 또는 변환의 family $b_1(X),b_1(X),....b_1(X)$ 를 가지는 것이다. X의 선형 모델을 적합하는 대신 아래 식 5 의 모델을 적합한다.

식 5) $y_i = \beta_0 + \beta_1b_1(x) + \beta_2b_2(x) + \beta_3b_3(x) + ... + \beta_Kb_K(x) + \epsilon_i$

기저 함수들은 선택되어 있다. 다항식 회귀의 경우 $b_j(x_i) = x_i^j$ 이고, 조각별 상수의 경우에는 I(.) 가 그것이다. 식 5는 설명변수로 기저함수를 가지는 표준보델로 생각될 수 있다. 따라서 회귀계수 추정에 최소제곱법을 사용 가능하다.

이것은 선형모델들에 대한 모든 추론도구들을 사용할 수 있다는 뜻 이다.

7.4 회귀 스플라인

회귀 스플라인은 X의 전체 범위에 걸친 고차원 다항식을 적합하는 대신, X의 범위를 구분하여 각 범위에 저차원 다항식을 적합한다. 여기서 계수들이 변하는 지점을 knots 라고 부른다.

점 c에서 단일 knot를 가지는 조각별 삼차 다항식은 다음의 형태를 가진다.

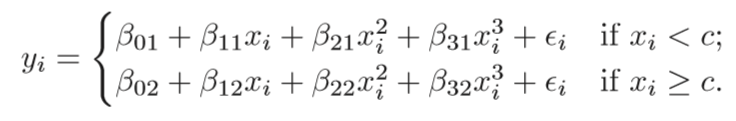
임시 이미지

즉, 두개의 서로 다른 다항식을 c를 기준으로 나눈 부분집합에 적합한다.

매듭(knots)을 더 많이 사용하면 조각별 다항식이 더 유연해진다.

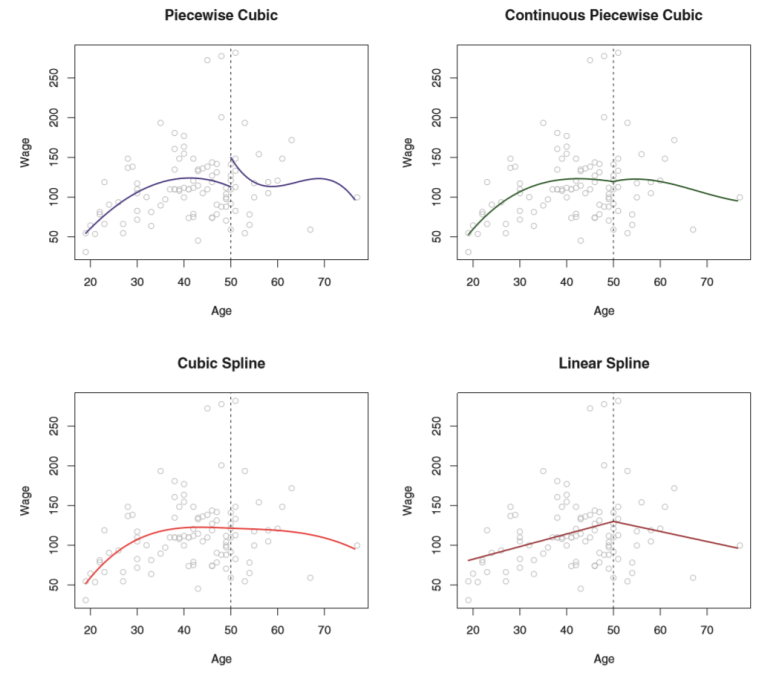
임시 이미지2

위 그림에서 좌상단의 그래프는 연속되지 않으므로 잘못된것으로 보인다. 이를 위해 적합 곡선이 연속적이어야 한다는 조건하에서 조각별 다항식을 적합할 수 있다. 이렇게 적합한 결과는 우상단의 그래프와 같이 나타난다. 하지만, 접합부가 v자 모양으로 꺾여있으므로 여전히 불연속적으로 보인다.

좌하단 그래프는 이를 위해 두가지 제한조건을 추가한 그래프이다. 이제 조각별 다항식의 도함수는 age = 50 에서 연속적이다. 이를 삼차 스플라인이라 불린다. 일반적으로 K개 knots를 가지는 삼차 스플라인은 총 4+K 자유도를 사용한다.

K개 knots를 가지는 회귀 스플라인의 기저는 식 6 과 같다. 따라서 최소제곱을 사용하여 적합 가능하다.

식 6 $y_i = \beta_0 + \beta_1b_1(x_i) + \beta_2b_2(x_i) + ... + \beta_{K+3}b_{K+3}(x_i) + \epsilon_i$

식 6 를 활용하여 삼차 스플라인을 나타내는 가장 직접적인 방법은 삼차 다항식에 대한 기저를 가지고 매듭 당 하나의 절단 멱함수 를 추가하는 것이다.